L’essentiel est invisible pour les yeux1
Exemples de modélisations implicites
Bernard Chabloz
&
Alaric Kohler
Haute École Pédagogique BEJUNE
Pour citer ce document
Introduction
Les exemples présentés ci-dessous soulèvent des questions qui pourraient être des tâches pour des élèves en physique. Nous avons sélectionné ces quelques exemples parce qu’ils permettent d’illustrer un lieu commun de l’apprentissage des sciences : ce que l’élève doit précisément apprendre reste invisible ou implicite. Ceci n’est évidemment pas une critique – et pour cause les exemples ci-dessous sont présentés hors contexte, de telle sorte qu’il ne s’agit pas de commenter la manière dont ces questions sont posées, travaillées, commentées, etc. Notre propos est plus général : les ressources sémiotiques utilisées en classe de science – et il en faut ! – ne jouent pas seulement le rôle d’outils sémiotiques permettant de réfléchir, résoudre des problèmes et proposer des prédictions, mais elles sont aussi – et même prioritairement pour ce qui est des élèves – des objets à interpréter, au sujet desquels peuvent apparaître des malentendus. Nous tenterons de montrer ici quelques illustrations du rôle que joue la modélisation dans ces implicites, qui ne sont pas toujours facilement interprétés.
Les deux premiers exemples portent sur des représentations visuelles. Celles-ci paraissent simples, mais elles mettent nos premières impressions au défi des réponses contre-intuitives de la physique. Notre analyse consistera à montrer que ce caractère contre-intuitif s’explique notamment par la modélisation implicite qui a permis la construction de ces représentations plus ou moins visuelles. Nous montrerons que c’est au prix d’une attention spécifique à la modélisation qui sous-tend ces représentations que les élèves peuvent dépasser leurs premières impressions et, en même temps, véritablement comprendre les représentations offertes à leurs yeux comme des outils sémiotiques. En particulier, les deux premiers exemples mettent en évidence la nécessité dans ce processus d’interprétation du va-et-vient de la pensée entre des représentations diverses d’un phénomène pour reconstruire la modélisation implicite qui a permis de les construire.
Certaines représentations sont facilement intelligibles, par exemple une animation ou un film, et n’invite pas à une analyse en termes de modélisation – quand bien même il y a peut-être une modélisation à l’origine de la représentation – alors que d’autres sont des représentations dont la lecture nécessite visiblement une analyse : par exemple un graphique, un graphe de fonction. Les pratiques scolaires passent souvent de l’usage de l’une ou l’autre de ces représentations sans avertissement, laissant à l’implicite l’éventuel modèle ayant permis leur construction. L’élève peut ainsi être amené à deviner par lui-même qu’il faut s’engager dans une stratégie d’exploration visuelle spécifique, comme la comparaison de points précis, ou l’arrêt sur image à des instants précis d’une animation.
Le troisième exemple met en scène sous la forme d’un paradoxe un implicite qui est courant non seulement en physique, mais également dans d’autres disciplines. Le paradoxe permet de communiquer facilement ce qui se joue au niveau de l’interprétation, néanmoins la même ambiguïté est souvent bien plus redoutable dans le contexte d’une tâche scolaire où, justement, elle n’est pas explicitée par une mise en contradiction.
Les exemples 4 et 5 portent sur des lois de la physique, exprimées en formules algébriques ou vectorielles. Comme les représentations visuelles, ces objets sémiotiques doivent être interprétés par leur utilisateur avant qu’ils puissent en faire des outils pour répondre à une question, résoudre un problème, énoncer une prédiction, etc.
L’exemple 4 permet d’illustrer la modélisation implicite à l’origine de l’expression algébrique, et la manière dont elle conditionne l’usage correct d’une loi de la mécanique. Les difficultés d’interprétation qui peuvent surgir sont illustrées par le récit d’une situation de malentendu en classe de physique, au lycée.
L’exemple 5 met en évidence la modélisation qui est parfois nécessaire pour compléter une loi, lorsque celle-ci est utilisée à la frontière de son champ d’application. Nous prendrons comme exemple la loi de Coulomb pour calculer l’attraction entre un objet neutre et un objet chargé.
Premier exemple
Le problème
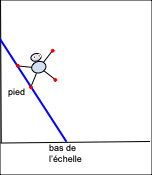
Toto est sur une échelle appuyée contre un mur. Soudain, le bas de celle-ci se met à glisser sournoisement et à s’éloigner du mur. Le haut de l’échelle reste appuyé au mur et Toto, pétrifié, reste accroché au même échelon.
Question :
Quelle est la trajectoire décrite par le pied gauche de Toto ?
Alors, qu’en pensez-vous ? Une idée, une impression ?
Vous pouvez la confronter à la trace de l’échelle présentée sur ce modèle GeoGebra (activez la boîte “trace de l’échelle” et déplacez le bas de l’échelle sur l’axe horizontal).
Il n’est pas impossible que votre première impression de la trajectoire du pied de Toto ressemble à la courbe que vous obtenez sur la construction GeoGebra en activant la trace de l’échelle…
La trajectoire du pied gauche de Toto est-elle dessinée par cette trace de l’échelle qui glisse ? Pour le vérifier, tentez une modélisation échelonnée dans le temps, en répondant successivement aux questions suivantes :
1. Dans quelle direction bouge le pied de Toto au début de la chute si l’échelle est appuyée (presque) verticalement ? Vous pouvez indiquer cette direction avec une flèche sur le schéma.
2. Dans quelle direction ce même pied arrive-t-il au sol au terme brutal de cette chute ? Là aussi, vous pouvez indiquer cette direction avec une flèche sur le schéma.
3. Quelle trajectoire pouvez-vous tracer pour représenter la réorientation progressive de la direction de la chute de Toto entre les deux moments analysés ci-dessus ? Cette question pourrait bien suffire à vous faire esquisser une trajectoire plutôt que la trace de l’échelle… Vous pouvez comparer votre trajectoire avec celle présentée (en rouge) sur le modèle GeoGebra (activez la boîte “trajectoire du pied” et déplacez le bas de l’échelle sur l’axe horizontal).
Si vous avez fini de jouer avec Toto et son échelle, et que vous voulez savoir pourquoi notre première impression nous conduit sur une fausse piste, vous pouvez lire le commentaire ci-dessous où nous expliquons pourquoi il s’agit, de notre point de vue, d’une modélisation implicite.
Commentaire2
En demandant de décrire la trajectoire de l’échelle, nous demandons en fait à l’élève d’effectuer une modélisation3. Cette demande de modéliser la trajectoire reste cependant implicite, à moins bien entendu de le préciser verbalement ou de jalonner l’exercice de diverses étapes comme nous l’avons fait ci-dessus avec les questions 1-3.
La difficulté de l’exercice s’explique notamment par le caractère implicite de cette demande. En effet, lorsque la modélisation n’est pas l’objet de l’attention conjointe de l’enseignant et de l’élève, ce dernier oriente son attention comme il le fait d’habitude. Or, quand on observe une échelle glisser c’est effectivement l’échelle qui attire notre attention. Personne n’observe les pieds d’un éventuel Toto alors que l’échelle chute… à moins peut-être que celui-ci n’ait décidé de porter une chaussure rouge particulière bizarre ? Essayez sur le modèle GeoGebra pour vous en convaincre : activez la trace de l’échelle et effectuez le glissement de l’échelle sur le plan horizontal, mais concentrez votre attention sur le point rouge du pied gauche de Toto. Vous verrez alors la trajectoire que la question initiale vous demandait implicitement de modéliser…
L’inadéquation de la première impression s’explique par une direction de l’attention différente. Or, quand bien même la question fait verbalement référence au pied de Toto, elle exige une démarche de modélisation qui demeure implicite : il s’agit d’analyser les positions successivement occupées par le pied de Toto et/ou par un échelon spécifique de l’échelle, et non l’espace visuel occupé par l’ensemble échelle-Toto qui attire notre attention parce qu’il est imposant. Dans le modèle GeoGebra, la “trace de l’échelle” est une représentation de cette occupation générale de l’espace visuel. Cette trace correspond à une première impression concernant la trajectoire de l’ensemble (dont le pied de Toto), parce que dans la vie quotidienne, notre exploration visuelle ne s’oriente pas d’emblée vers un objet spécifique, mais se laisse guider par ce qui attire l’attention et/ou aborde la situation dans son ensemble, de manière indifférenciée (au moins dans un premier temps).
Deuxième exemple
Sur cette animation GeoGebra, observez l’oscillation des deux balanciers.
● Lequel des deux a-t-il un mouvement qui vous paraît “normal“?
● Notez les remarques que ces mouvements suscitent chez vous.
● Dessinez une représentation graphique du mouvement de chaque balancier sur un graphe qui représente l’angle du fil du pendule en fonction du temps.
Vous pouvez confronter votre graphe à celui que vous voyez apparaître en cochant la case correspondante sur l’animation GeoGebra. L’animation permet de travailler à la traduction entre les deux représentations : l’évocation du mouvement du pendule qui se balance et le graphe de l’horaire (l’angle en fonction du temps). Dans la première représentation, la droite représente le fil du pendule et indique son angle, alors que dans la seconde la droite noire représente le temps qui s’écoule (une grandeur physique comportant une unité), et les tracés colorés les valeurs des angles (grandeur sans unité) aux différents moments.
Dans cet exemple, nous avons tenté de rendre explicite à l’aide d’une animation GeoGebra et de quelques commentaires ce qui constitue souvent une modélisation implicite dans les pratiques scolaires : que l’on présente une image de pendule pour schématiser ou illustrer un problème, ou que l’on demande aux élèves de travailler sur des graphes, le processus de modélisation permettant d’interpréter le sens des tracés n’est souvent pas discuté ou analysé explicitement. En conséquence, ce qui signifient ces divers tracés échappe souvent à une compréhension suffisante à leur reconstruction et à leur emploi comme outils sémiotiques pour penser des problèmes concrets, c’est-à-dire pour modéliser d’autres situations.
Troisième exemple
Considérez l’énoncé suivant :
Plus il y a de fromage, plus il y a de trous. Mais plus il y a de trous, moins il y a de fromage. Donc plus il y a de fromage, moins il y a de fromage.
L’absurdité de ce syllogisme vient bien sûr de l’ambiguïté liée aux comparatifs plus et moins, selon que leur référent est une grandeur extensive (la quantité de fromage) ou intensive (la densité du fromage). L’énoncé paradoxal force la distinction entre grandeur extensive et grandeur intensive. Les premiers fromage et trou sont en effet extensifs, ce sont des quantités. Ils sont cumulables, additifs, et l’un croît si l’autre en fait autant. Les seconds sont intensifs, ce sont des densités, et en effet, la densité du fromage diminue si la densité de trou augmente…
Quatrième exemple
La loi de la gravitation universelle de Newton peut s’exprimer par l’équation suivante:

Cette équation permet de calculer g à la surface de la Terre : il suffit de remplacer par la masse de la Terre et par son rayon. Voilà un traitement “scolaire”, une anodine manipulation de formule qui passe sous silence le geste modélisant qui l’autorise : cette loi ne s’applique en effet qu’à des points matériels. Cette idéalisation ou simplification a été introduite au cours de la modélisation qui a permis à Newton de définir mathématiquement la force de gravitation, tout en reconnaissant par ailleurs ne pas savoir ce qu’elle est réellement4.
Un regard expérimenté sur la formule remarquera d’ailleurs que cette condition d’application de la loi figure dans son écriture : si l’on ne considère par la Terre comme un point matériel situé au centre de gravité de la planète, et l’autre objet attiré et attirant la Terre comme un autre point matériel, alors il n’y a pas de distance entre eux, autrement dit n’est pas défini !
Quand bien même il est possible de déduire la contrainte d’application à partir de l’écriture de la loi, une partie de la modélisation demeure implicite en ce sens que la seule référence de à la notion de distance n’explicite pas que les objets sont traités comme des points matériels, dans quelles conditions il est permis de les traiter ainsi, etc. D’autant plus que l’on ne peut pas vraiment tenir pour anodin le fait de considérer la Terre comme un point matériel… Ainsi, la modélisation implicite à la loi exprimée par l’équation ci-dessus pourrait conduire à des interprétations diverses et variées. En voici un exemple brièvement exposé.
Exemple de malentendu
La situation de malentendu reportée ici est présentée de manière plus complète dans le travail de recherche dont elle est issue5, en particulier pour ce qui est de la séquence d’enseignement et du contexte de la classe de physique.
Nous sommes dans un lycée suisse, un gymnase, lors d’un cours de Physique. Les élèves ont effectué un exercice demandant de calculer la force d’attraction exercée par la Lune sur la Terre à l’aide de la loi de la gravitation universelle citée ci-dessus. Pour cet exercice, les élèves ont reçu des valeurs pour la masse de la Terre, le rayon de la Terre, la masse de la Lune, le rayon de la Lune et la distance entre la Terre et la Lune. L’exercice suivant a pour consigne :
“ Extraire l’expression de g et calculer sa valeur”.
Dans un premier temps, la deuxième loi de Newton F = ma permet de définir l’accélération en relation à la somme des forces. Seule la force de gravitation est considérée dans cet exercice. Ensuite, il s’agit justement pour les élèves d’utiliser la loi de la gravitation universelle en traitant la Terre comme un point matériel, et n’importe quel objet à sa surface comme un autre point matériel, la distance entre ces deux points étant le rayon de la Terre. La résolution mathématique peut s’écrire:
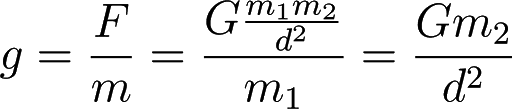
En remplaçant par les valeurs données pour la constante G, la masse de la Terre (m1) et le rayon de la Terre (d), on obtient g = 9.79m/s2.
Une des élèves de la classe, au lieu de procéder ainsi, utilise la Lune de l’exercice précédent comme objet attiré par la Terre pour extraire g. Elle utilise la distance Terre – Lune pour d et obtient g = 0.01m/s2 . Cette élève a répondu correctement à l’exercice précédent et réussit généralement à produire la “bonne réponse“, disposant d’une bonne moyenne dans cette branche d’enseignement. Néanmoins, la situation de malentendu brièvement rapportée ici démontre un usage de la loi de la gravitation universelle sans comprendre : l’interprétation que cette élève fait de son expression, et en particulier de d, fait l’impasse sur la modélisation implicite à l’origine de la loi de la gravitation universelle. La distance est interprétée comme une valeur donnée dans l’exercice, au même titre que G, pour laquelle cette interprétation est pertinente puisqu’il s’agit d’une constante. Ainsi, la modélisation de l’objet quelconque à la surface de la Terre en tant que point matériel situé à une distance d’environ le rayon de la Terre du centre de gravité de la Terre, et de la Terre en tant que point matériel situé au centre de gravité de la Terre, n’a pas été comprise.
Cinquième exemple
La loi de Coulomb peut s’exprimer par l’équation suivante:
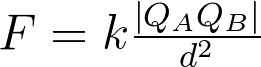
Elle ne paraît pas en mesure de prédire l’attraction d’un objet neutre par un objet chargé, puisqu’elle aura systématiquement une valeur nulle lorsqu’une des deux charges est nulle. C’est pour la même raison qu’à l’exemple 4 : la Loi de Coulomb ainsi écrite ne s’applique qu’à des charges ponctuelles, ce qui est encore plus clair si on l’écrit:
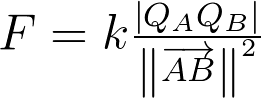
Les points A et B ne sont pas définis dans le cas de charges… non ponctuelles.
Ici encore, la seule lecture de ces équations ne conduira pas facilement l’élève aux commentaires que nous venons de faire : la modélisation doit être explicitée pour qu’il puisse comprendre les conditions d’application de la loi de Coulomb et se l’approprier comme un outil sémiotique pour résoudre un problème, répondre à une question, etc.
Pour appliquer la loi de Coulomb à l’attraction entre un objet neutre et un objet chargé, la modélisation doit être complétée par deux hypothèses :
1. l’objet chargé polarise l’objet neutre, qu’on considère alors comme deux charges ponctuelles opposées ;
2. la loi de Coulomb est correcte lorsqu’elle prédit que l’attraction (entre l’objet chargé modélisé par une charge ponctuelle et la charge du dipôle la plus proche) l’emporte sur la répulsion (avec l’autre charge du dipôle).
Remarquons que, sans la loi de Coulomb, l’observation du phénomène d’attraction d’un objet neutre par un objet chargé peut conduire à une modélisation en deux hypothèses semblables :
1. l’objet chargé polarise l’objet neutre, qu’on considère alors comme deux charges ponctuelles opposées ;
2. le phénomène observé implique que l’attraction l’emporte sur la répulsion.
En conséquence de ces deux hypothèses, on peut en déduire que la force électrostatique est décroissante en fonction de la distance entre les charges, ce qui est ni plus ni moins l’énoncé approximatif de… la loi de Coulomb !
Conclusion
Nous avons discuté ailleurs dans ce dispositif d’enseignement mi-fini de l’importance, pour un apprentissage de la modélisation, d’activités et de décisions relatives à la modélisation effectivement menées par les élèves. Dans les quelques exemples exposés ci-dessus, nous avons pu montrer que la modélisation est présente en physique même sans un dispositif d’enseignement explicitement centré sur cet objet, et même si l’enseignant n’attire pas l’attention sur cette dimension de la discipline. C’est pourtant une raison d’aborder la modélisation explicitement et de mettre en oeuvre des séquences d’enseignement où les élèves peuvent s’engager activement dans la construction de modèles, plutôt qu’une raison de penser que la modélisation est de toute façon travaillée en classe de science. En effet, les exemples ci-dessus suggèrent que les élèves sont confrontés à des modélisations implicites lorsqu’ils sont dans le rôle d’interprétant de ressources sémiotiques comme les graphes, les notions ou concepts fondamentaux (nous avons pris l’exemple de la distance), et les équations. Or, pour apprendre à interpréter ces objets sémiotiques avec pertinence, il paraît essentiel de pouvoir s’engager activement à les construire et à les déconstruire. Sans un travail de montage et démontage des ressources sémiotiques proposées, la seule lecture et l’usage strictement scolaire de ces mêmes ressources risquent de conduire les élèves à effectuer leurs tâches (peut-être) avec succès, mais sans comprendre…
[1] De Saint-Exupéry, A., (1943). Le Petit Prince. New-York: Reynal & Hitchcock.
[2] Ce commentaire prend appui sur des éléments de psychologie de la perception.
[3] Le terme modélisation désigne ici l’opération cognitive effectuée par l’élève, et les éventuelles activités sociales et sémiotiques qu’il met en oeuvre en soutien à ses opérations cognitives (interaction avec ses pairs, dessin d’esquisses et de schéma, etc.).
[4] Pour une discussion de la distinction entre la question de la nature de la force de gravitation en Philosophie de la Nature, et la question de la définition mathématique, voir par exemple : Koyré, A., (1968). Etudes newtoniennes. Paris: Gallimard.
[5] Cette situation est empruntée à la recherche doctorale de A. Kohler (non publiée), intitulée “Approches psychologiques de situations de malentendu dans des activités de didactique des sciences” et soumise à l’Université de Neuchâtel, Suisse.

