Alaric Kohler
&
Bernard Chabloz
Haute École Pédagogique BEJUNE
Pour citer ce document
Introduction
Les notions de modèle et modélisation, quoique fondamentales pour la démarche scientifique, ne sont pas toujours utilisées dans le même sens, et bénéficient rarement d’une définition explicite dans les travaux de didactique des sciences. De plus, des études récentes suggèrent un manque de formation dans ce domaine chez les enseignants. Par exemple, Roy et Hasni (2014) se sont intéressés aux représentations qu’ont des enseignants du secondaire au Québec de la modélisation. Ils mettent en évidence que c’est un objet d’enseignement qui n’est souvent que partiellement compris et dont les finalités pour l’enseignement des sciences ne sont souvent pas claires du point de vue des enseignants. Ce qui semble surtout manquer selon cette étude, c’est une compréhension épistémologique de ce qu’est un modèle: comment il se construit, quel est son rôle dans le développement de la connaissance scientifique et comme outil de travail du physicien, et comment il peut constituer la clef de voûte d’une approche pédagogique. Par exemple, les auteurs soulignent que le modèle scientifique est surtout pensé comme un système d’explication du monde, plutôt que comme l’occasion pour les élèves de travailler avec leurs savoirs conceptuels à leur niveau de compréhension, et pour l’enseignant d’en faire une évaluation diagnostique de ces savoirs.
L’activité cognitive de modélisation reste également peu fréquente dans l’enseignement de la physique pour les élèves selon une étude de Luc & Durey (1997), et cela malgré le fait que certaines séquences soient construites dans cette intention, notamment durant les leçons de « travaux pratiques ». Ces auteurs comparent des séquences d’enseignement prenant pour objet le fonctionnement d’un haut-parleur afin de documenter les diverses pratiques de modélisation en travaux pratiques de physique. Ils se posent la question de la traduction des « curriculums prescrits » en « curriculums réels », et soulignent le fait que « de façon quasi générale, la problématisation des savoirs à enseigner mis en scène dans les séquences observées n’est pas clairement explicitée aux élèves » (p.53). Autrement dit, le lien entre le modèle quantitatif de ce qui constitue l’objectif du curriculum (dans l’exemple discuté, c’est la force de Laplace, «F = k i ») et le haut-parleur en tant qu’objet technique du quotidien est le plus souvent implicite. En conséquence, la question de l’établissement du lien entre les grandeurs « F » et « i », permettant de calculer la constante k à partir d’une étude du haut-parleur, est une préoccupation de l’enseignant que des élèves peinent à s’approprier. Cela tient notamment au fait que c’est l’enseignant qui dirige le raisonnement, partant certes d’un objet concret – le haut-parleur -, mais en déplaçant de sa propre initiative le sujet de conversation sur un aspect abstrait très spécifique – la proportionnalité entre les variables « F » et « i » -. La discussion porte donc sur un modèle établi en physique plutôt que sur l’objet concret.
Un autre résultat de cette recherche consiste à montrer que la partie « pratique » des séquences prend presque toujours (huit fois sur neuf) la forme d’activités expérimentales des élèves en binômes, où ils doivent suivre un protocole (une procédure) écrit par l’enseignant de manière à faire varier certaines valeurs et reporter des mesures. Cette partie du travail des élèves est celle à laquelle toutes les séquences consacrent largement le plus de temps (entre 43 et 69 minutes dans l’étude citée), alors que la problématisation ne dure que quelques minutes au plus. Les séquences analysées par les auteurs sont construites sous la forme d’une succession d’étapes de durées très variables, dans un ordre donné par l’enseignant, et dont les liens restent le plus souvent implicites. La plupart des séquences débutent par une amorce de l’ordre de la monstration d’un phénomène, et se terminent par « l’établissement du modèle expérimental F = k i » à la suite d’interprétations du fonctionnement du haut-parleur qui se basent essentiellement sur des raisonnements analogiques, sauf pour trois des neuf séquences où le fonctionnement du haut-parleur n’est pas du tout interprété.
Les auteurs tirent des conclusions quant aux compétences des enseignants et à leurs difficultés relativement à la mise en œuvre d’activités de modélisation. Toujours selon les auteurs, les enseignants « savent conduire la démarche d’établissement d’un modèle expérimental », et sont conduits par des « coutumes pédagogiques classiques de l’enseignement des sciences physiques au lycée selon lesquelles les expériences de monstration, les protocoles, les conclusions relèvent de tâches du professeur, alors que les tâches les moins nobles d’exécution de montages, mesures, tracés, calculs relèvent des élèves » et par les « contraintes de l’évaluation » (F = k i permettant de construire facilement des exercices graphiques et numériques classiques pour l’évaluation sommative). Par contre, pour expliquer les pratiques étudiées, les auteurs proposent diverses hypothèses qui seraient des difficultés pour les enseignants ou des défis spécifiques posés par l’activité de modélisation. Selon ces hypothèses, les enseignants conduiraient leurs séquences à la manière décrite ci-dessus parce qu’ils ne maîtrisent pas :
● « les démarches relatives à l’étude d’un objet technique de la vie quotidienne » ;
● « l’application du modèle F = k i au contexte du fonctionnement du haut-parleur », dans toute la complexité de l’objet technique ;
● « l’épistémologie de la physique » qui les induit à penser que l’étude du haut-parleur, ce n’est pas « de la physique », et qu’il faut étudier quelque chose de moins contingent comme le modèle «F = k i ».
D’autres résultats plus détaillés de cette recherche mériteraient d’être repris pour la préparation d’activités d’apprentissage des élèves qui soient effectivement modélisantes.
Nous proposons ici une brève revue de la littérature qui aborde la modélisation, de manière non exhaustive, dans le but de dégager quelques nuances dans l’acception du concept de modèle et de modélisation et de mettre en évidence quelques divergences dans les définitions proposées en didactique des sciences.
Travailler sur ou à partir de modèles scientifiques
Une manière d’envisager la modélisation en didactique des sciences consiste à faire travailler les élèves sur des modèles scientifiques établis, ou à utiliser ces modèles comme points de départ de leurs activités. Par exemple, la tâche des élèves consiste à mettre en place une expérience ou série de mesures permettant de confirmer (ou non) le modèle présenté par l’enseignant.
Gilbert (2013) distingue quatre approches faisant usage de modèles scientifiques dans l’enseignement :
1. La première consiste à apprendre des modèles faisant partie du curriculum, qui font ou ont fait l’objet d’un consensus à une époque historique donnée. L’engagement des élèves dans ce type d’approche reste très limité, selon l’auteur, à moins d’inviter les élèves à des raisonnements analogiques sur des phénomènes qu’ils connaissent bien, ou de présenter le fil narratif permettant de dégager les enjeux historiques et philosophiques du modèle dans son contexte d’émergence.
2. La seconde approche consiste à faire usage de modèles enseignés dans diverses tâches, de manière à confronter les élèves à la question du transfert: quand bien même ils auraient bien compris le modèle enseigné, dans une tâche nouvelle l’usage du modèle peut leur poser de nouveaux défis.
3. La troisième approche consiste à faire réviser les modèles enseignés, par exemple en cherchant à étendre leur domaine d’application à des situations pour lesquelles il n’est pas évident qu’ils soient adéquats. Dans cette démarche, les élèves doivent entrer en matière dans la construction d’un modèle, quoique toujours en partant d’un modèle enseigné.
4. La quatrième approche consiste à faire reconstruire par les élèves le modèle conventionnel, présumé correct ou consensuel. Pour assurer le guidage nécessaire de cette intention pédagogique, les élèves ne partent pas de rien, mais reçoivent diverses ressources (données, graphes, etc.), questions et feed-back qui ont pour but de les orienter vers le “bon” modèle. Dans cette approche, le contenu du modèle est donc connu des élèves, qui ont pour tâche de lui donner une forme adéquate et éventuellement créative.
5. La cinquième approche consiste pour les élèves à apprendre à construire un nouveau modèle, à partir d’un phénomène librement choisi ou transmis par l’enseignant. Ce sont les élèves qui doivent se poser les questions permettant de construire le modèle, et mettre en place une éventuelle démarche permettant de l’éprouver.
Les approches 1 et 2 n’engagent pas les élèves à une activité de modélisation, sinon peut-être sous une forme passive et imaginative “pour comprendre” le discours enseignant. Avec l’approche 3 apparaît la question de la modélisation par l’élève, encore qu’il ne construit pas un modèle, mais a pour tâche de modifier, transformer ou adapter un modèle présenté et expliqué par l’enseignant. Dans l’approche 4, les élèves sont invités à s’engager dans une activité de modélisation, mais comme il s’agit de reconstruire un modèle défini par l’enseignant à partir d’éléments donnés, le processus de modélisation n’est que partiellement conduit par l’élève voire pas du tout, si l’élève interprète le jeu didactique proposé comme un jeu de devinette des attentes. Il n’y a donc que la cinquième et dernière approche qui requiert une activité de modélisation de l’élève, comme l’auteur le souligne lui-même.
Ces cinq approches permettent de distinguer avec une gradation en quoi la modélisation est un objet d’enseignement : la modélisation est-elle l’objet de conversation, la thématique abordée? Les approches 1 et 2 décrites ci-dessus abordent effectivement la modélisation, mais guère plus que comme thématique générale, alors que dans les approches 3 et 4 les élèves travaillent les modèles présentés. La modélisation n’est pas seulement ce dont on parle, mais un objet, un outil auquel on s’intéresse. Ce n’est cependant que dans la cinquième approche que les élèves s’engagent eux-mêmes dans une activité de modélisation.
La modélisation en tant qu’activité créative
Nous venons juste de faire la distinction entre la modélisation en tant que sujet de conversation, thématique, et en tant qu’activité effective des élèves. Comment peut-on définir l’activité de modélisation?
Il s’agit d’un exercice d’imagination: le modèle s’invente. Mais il s’agit aussi d’une production: le modèle produit par les élèves est un ensemble de signes organisés qui peut se décrire, en langage verbal et/ou mathématique, et/ou par des esquisses, schémas, graphiques, ou autres représentations plus ou moins complexes. Ce sont là les caractéristiques d’une activité créative. Une des manières de le mettre en évidence consiste à constater la diversité des productions au sein d’une classe qui a pour tâche de construire un modèle. Les activités créatives ont pour particularité (Giglio, 2015) de comprendre des processus indissociables du produit et des relations que l’agent entretient avec d’autres personnes, éventuellement une société dans son ensemble. Ces relations déterminent un champ de tension qui est une partie constitutive de l’activité créative. Elles déterminent notamment la question de l’originalité et de la nouveauté, bien que Giglio (2015) souligne aussi la possibilité lors d’une activité créative d’un agent qui produit quelque chose qui n’est nouveau que de son point de vue. Cette remarque concerne les processus psychiques en jeu lors d’une activité créative: cette nouveauté indique qu’en s’engageant dans une activité créative, l’élève accepte de travailler en vue d’un produit qu’il n’est pas d’emblée capable de se représenter terminé.
Nous avons brièvement dégagé trois dimensions de l’activité créative, que nous pouvons décliner pour la modélisation :
1. le produit, qui renvoie d’une part à la question de la définition de ce qu’est un modèle;
2. les processus, qui renvoient notamment aux opérations cognitives mises en oeuvre lors de l’activité, mais aussi aux dialogues, aux sentiments et émotions, etc.;
3. les relations sociales et symboliques sous la contrainte desquelles l’activité est guidée. Concernant la modélisation en physique, nous aborderons cette dimension du point de vue sémiotique plutôt que social, les contraintes déterminant l’acceptabilité et l’originalité d’un modèle étant plutôt symboliques (conventions d’écriture, liens avec les concepts et théories de référence de la discipline, etc.) que sociales, au moins en milieu scolaire (la question de l’acceptation par la communauté scientifique des physiciens n’étant pas pertinente).
Qu’est-ce qu’un modèle? Éléments d’épistémologie
Considérer le modèle en tant que produit d’une activité nous invite à discuter ce qu’est un modèle.
Une diversité de modèles
Huber et Tytler (2013) mettent en évidence divers sens donnés au modèle en science, à partir de la littérature anglo-saxonne, soulignant la diversité des définitions, la pluralité des typologies de modèles. Par exemple, Gilbert (cité par Huber et Tytler, 2013) présente la classification suivante des modèles:
● les modèles concrets comme les figurines ou modèles réduits;
● les modèles graphiques et picturesques comme les photographies, diagrammes;
● les modèles mathématiques, par exemple les formules, graphiques ou cartes topographiques;
● les modèles verbaux tels que les descriptions, scripts;
● les modèles de simulation, comme les jeux de simulation, les poupées des crash tests;
● les modèles symboliques ou “sémiotiques”, comme les mots, les nombres ou les figures mathématiques.
Cette première typologie comprend de zones de recoupement : la poupée du “crash test” appartient au modèle de simulation, mais aussi au modèle concret, les modèles mathématiques et modèles verbaux sont aussi des modèles symboliques. De plus, tous les modèles peuvent être définis comme des systèmes symboliques, à l’exception peut-être des modèles concrets1. Ainsi, les critères de la typologie de Gilbert ne semblent pas se situer tous au même niveau. Black (cité par Huber et Tytler, 2013) présente une typologie plus économique, comprenant quatre types de modèles :
● les modèles à l’échelle;
● les modèles analogiques;
● les modèles théoriques;
● les modèles mathématiques.
Les modèles à l’échelle reprennent l’idée du modèle réduit, les modèles analogiques comprennent les photographies, les jeux de simulation (qui peuvent être complétés par un modèle mathématique dans certains cas) et certaines métaphores (comme le modèle du traitement de l’information) alors que les modèles théoriques constituent une catégorie de modèles dont le rôle est de représenter un (ensemble de) phénomène(s). Lorsque cette représentation permet des prédictions quantitatives, il s’agit d’un modèle mathématique. La question de savoir si le modèle mathématique est une sous-catégorie du modèle théorique pourrait être discutée ici, cependant les deux types de modèles ont clairement leur spécificité : le modèle théorique constitue un système symbolique plutôt centré sur l’explication alors que le modèle mathématique est centré sur des prédictions ou simulations numériques, parfois sans même chercher à expliquer les phénomènes modélisés (p. ex. les modèles statistiques qui n’ont aucune visée explicative).
Dans cette typologie, c’est la forme que prend le modèle qui détermine le type : forme concrète et matérielle pour les modèles à l’échelle, forme métaphorique ou picturesque pour les modèles analogiques, forme d’une théorie (comprenant éventuellement divers langages et représentations visuelles) pour le modèle théorique, et forme mathématique pour les modèles mathématiques.
Winther (2006) reprend cette typologie de Black pour en fournir une explication plus détaillée, et une mise en perspective historique. Il propose également des exemples qu’il serait intéressant d’analyser plus en détail, et des propositions d’activités en classe “sur modèles et modélisation” (p.627). Martinand (1996) propose également une définition schématique de la modélisation en vue d’un usage dans l’enseignement des sciences, ayant pour inspiration ce qui se fait dans l’enseignement de la technologie. Ce lien avec la technologie et les sciences de l’ingénieur mériterait une discussion spécifique.
Modèles et représentation
Oh et Oh (cité par Huber et Tytler, 2013) soulignent que la multiplicité des modèles va de pair avec les multiples formes de représentations et modes sémiotiques utilisés dans leur construction. Face à cette diversité, Huber et Tytler (2013) soulignent un point de convergence qui est la proximité entre modèle et représentation (au sens sémiotique, ici selon Peirce) : le modèle est construit comme un signe (complexe) représentant certains aspects d’un système. Le modèle, selon ces auteurs, est toujours moins riche que ce qu’il représente, sans quoi ce serait une copie (p.111). Par conséquent, il est toujours possible de construire des modèles différents représentant la même chose, que ce soit pour représenter des aspects différents ou pour répondre à une autre question ou un autre objectif.
L’approche sémiotique présentée brièvement ici met en évidence ce qui est peut-être la caractéristique la plus importante concernant un modèle, à savoir que c’est un signe construit par l’être humain pour comprendre, expliquer et prédire le monde dans lequel il vit. Pourtant, l’analyse de l’objet modèle en tant que signe ne suffit pas à en souligner toutes les caractéristiques : pour bien comprendre ce qu’est un modèle, il convient aussi d’examiner comment il fonctionne, à quoi il sert dans les contextes spécifiques où il est utilisé. Il nous paraît dès lors intéressant de compléter l’approche représentationnelle des auteurs ci-dessus en mettant le modèle dans son contexte de la construction des connaissances scientifiques.
Modèles et théorisation
Grize propose une analyse des concepts de théorie et de modèle à partir des processus qui permettent leur construction logique, de manière à les distinguer précisément :
Un modèle peut être considéré comme une construction faite à propos de quelque phénomène et non pas simplement de ce phénomène. Ceci implique qu’un modèle ne repose pas directement sur des observables, mais sur un ensemble de concepts élaborés par ailleurs. (…)
Un modèle repose sur des hypothèses qui sont comme une sorte d’essai au sein d’une théorie où elles sont formulées. (…)
Un modèle devient alors une représentation autonome, c’est-à-dire un objet de pensée fermé sur lui-même et qui n’est ni amputable, ni résumable. Tel n’est pas le cas de la théorie qui lui sert de base. Celle-ci est toujours de l’ordre des schématisations et contient donc en elle le principe de son évolution.
(Grize, 1996, p. 52-53)
Dans ce passage, Grize propose une définition du modèle qui le contextualise dans le processus plus général de théorisation : Grize fait référence à une théorie avant son axiomatisation, et l’oppose au modèle par le fait de ne pas être autonome. Le modèle se définit ainsi comme le point d’aboutissement de ce processus, lorsque la théorisation est terminée et qu’elle peut être axiomatisée (cf. figure 1).
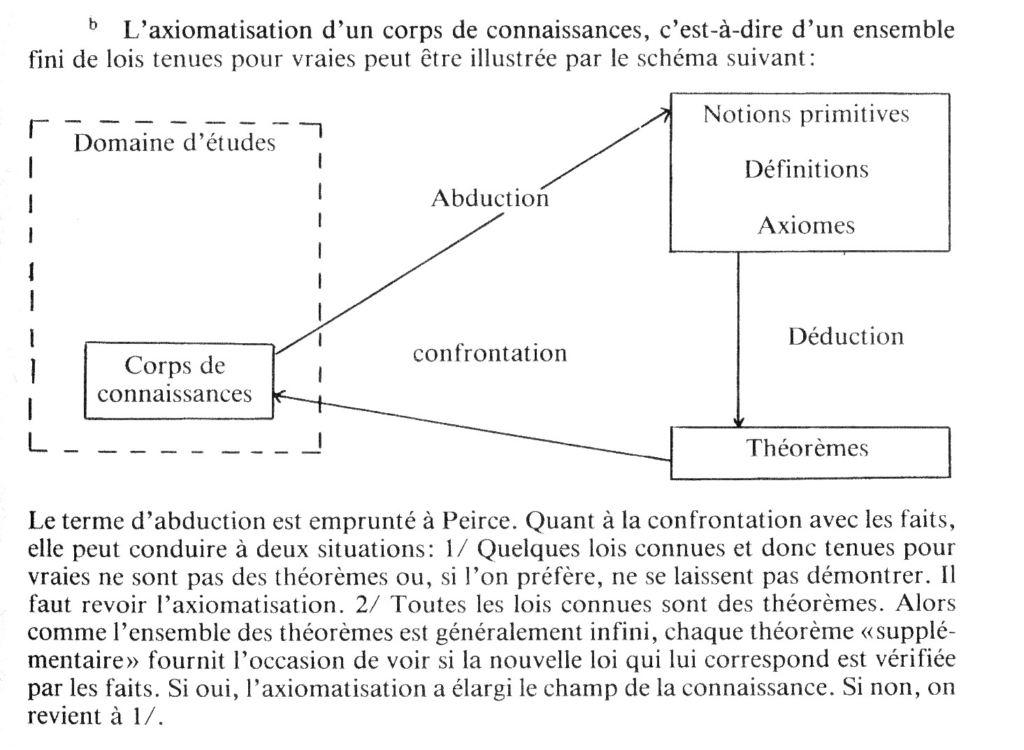
Figure 1. Brève explication du processus d’axiomatisation dans la construction d’une théorie, extrait de Grize, 1982, p.39.
Le modèle, produit de l’axiomatisation, échappe à toute vérification empirique, car il est désormais isolé du processus de théorisation qui a permis sa construction. En effet, si le modèle peut se conserver malgré le phénomène, pour ainsi dire, la théorie doit de son côté s’y adapter. Ainsi, une théorie sera complétée, amendée ou révisée lors de faits nouveaux mis en évidence par une observation utilisant cette même théorie pour rendre compte des faits, tandis que pour concevoir un dispositif d’ingénieur il n’est pas nécessaire de disposer d’une théorie, mais il faut construire un modèle permettant notamment des prédictions (la solidité du pont, etc.), peu importe après tout que ce modèle ne comprenne pas toute la complexité de la réalité qu’il modélise : c’est un “essai”, comme l’écrit Grize. Nous savons d’ailleurs aujourd’hui que si nous souhaitons effectivement nous intéresser à la valeur du modèle utilisé, c’est par une démarche différente que nous y parvenons, le plus souvent en boucle rétroactive entre construction du modèle et recherche permettant d’en documenter l’adéquation. À ce moment-là, une théorie est nécessaire, au moins pour définir cette “adéquation” du modèle construit à ce qu’il modélise. Ce problème de la vérification des modèles, que Grize réduit à la “détermination de procédures nécessaires à estimer leur adéquation aux phénomènes référentiels qu’ils représentent”. Grize ajoute cette précision utile en guise de synthèse :
En résumé, la distinction fondamentale entre les schématisations et les modèles, celle entre les jeux de langue et de langage, consiste en ceci que les premières restent en contact continuel avec le monde, tandis que les seconds s’en détachent totalement après les moments de leur élaboration.
(Grize, 1996, p. 54-55)
Comme les modèles sont associés aux “jeux de langage” et que, par ailleurs, un langage est par définition formel, les modèles sont bien des systèmes formels. Peut-être pouvons-nous comprendre l’utilisation du terme modèle dans cet ouvrage comme la volonté de simplifier quelque peu les propos et de bien distinguer entre théorie non constituée en système formel et théorie axiomatisée et constituant un système formel, utilisant le concept de théorie pour la première et de modèle pour la seconde. Cette analyse de Grize nous permet de brièvement présenter la distinction entre théorie et modèle au fil du processus de théorisation :
— tout ensemble d’énoncés vrais relatifs à des objets donnés est une théorie,
— une théorie est une schématisation,
— elle contient le principe de son évolution,
— cette évolution est le processus de théorisation,
— c’est la théorisation qui amène du nouveau dans la connaissance et non la théorie,
— une théorie peut être axiomatisée,
— une théorie axiomatisée peut être formalisée,
— une théorie formalisée étant fermée, elle n’amène plus rien de nouveau, elle n’est pas un processus, ni une schématisation : elle est un modèle.
L’analyse de Grize de la distinction entre modèle et théorie met en évidence l’importance d’une distinction entre le processus de construction d’un modèle et le modèle en tant que construit axiomatisé. Cette distinction épistémologique est nécessaire pour l’enseignant aussi, car la modélisation travaillée en classe concerne forcément à la fois la théorisation et les modèles construits : les élèves doivent comprendre et apprendre à utiliser des modèles, mais pour les comprendre il est nécessaire de revenir sur, voire de participer au processus de théorisation qui a permis de les établir. En effet, ces modèles enseignés étant axiomatisés, ils ne représentent plus les phénomènes au sens d’une théorie réfutable et modifiable, et si les élèves n’ont pas l’occasion de faire du processus de théorisation ayant permis leur construction un objet d’apprentissage, les choix et raisonnement justifiant ces modèles demeurent implicites et, le plus souvent, incompréhensibles. Nous partons donc de l’hypothèse, dans notre analyse, que c’est en participant au bricolage sémiotique à l’œuvre dans la construction des modèles que les élèves peuvent, d’une part, comprendre les modèles axiomatisés enseignés en classe et, d’autre part, comprendre le processus de modélisation, qui est une forme particulière de théorisation.
La modélisation en tant qu’activité sémiotique
Dans la recherche, il y a un intérêt grandissant pour une approche sémiotique de l’apprentissage des sciences, centrée sur l’usage de représentations visuelles et graphiques et sur la construction du sens par les élèves (p. ex. : Lund and Bécu-Robinault, 2010). Bécu-Robinault (2015) propose une démarche de conception et d’analyse d’activités de modélisation, qui met l’accent sur l’interprétation et l’activité créative des élèves, en particulier l’usage et la construction sémiotique. Ces travaux mériteraient d’être exposés plus en détail ici.
Tytler, Prain, Hubber et Waldrip (2013) proposent une démarche pédagogique centrée sur la construction de représentations. Le concept de représentation s’entend ici dans deux sens, explicitement distingués dans la conclusion de l’ouvrage en représentation externe et représentation interne (p.196). La représentation externe est une représentation au sens où elle représente quelque chose d’autre que ce qu’elle est (une image, un croquis, etc.). C’est la définition générale du signe, ce qui nous conduit à ranger cette approche comme s’intéressant à la sémiotique. Par ailleurs, un mot écrit sur un morceau de papier peut être considéré comme une représentation externe dans ce sens général, mais les auteurs se concentrent dans leur ouvrage sur les productions graphiques ou imagées, proposant comme synonyme de représentation externe la visualisation externe. La représentation interne fait quant à elle référence aux apprentissages des élèves, et/ou à des concepts des sciences cognitives comme celui de modèle mental (cf. ci-dessous), de concept (au sens d’un objet d’apprentissage), d’image mentale (Piaget). Cela fait référence aux représentations mentales que les élèves construisent au fil de leur apprentissage.
La représentation, en tant que propriété du signe, est abordée à l’aide de la conception triadique du signe de Pierce (p. ex. p.19), qui permet justement de mettre en évidence la distinction entre la signification construite par l’élève (représentations mentales), les signes utilisés (représentations graphiques, imagées, langagières, etc.) et l’objet réel ou objet du discours. Waldrip et Prain (ibidem) mettent en évidence l’intérêt pour les élèves de manipuler divers modes sémiotiques pour s’approprier les concepts, pour en construire le sens de manière à ce que cela soit en lien avec leur expérience personnelle, et pour permettre aux enseignants de mieux prendre conscience des interprétations diverses de leurs élèves. Ces auteurs soulignent quelques conditions qui leur paraissent nécessaires dans cette démarche pédagogique (p.26) :
● une bonne adéquation entre le but du mode sémiotique utilisée (“representational mode”) et la tâche de l’élève ;
● un étayage renforcé de l’activité des élèves par l’enseignant, en particulier concernant la négociation de la pertinence (“adequacy”) des représentations utilisées ;
● une compréhension, de la part des élèves, des formes et fonctions des représentations, de la pertinence de ces représentations et des liens qu’elles entretiennent avec leurs propres représentations mentales (“their understandings”).
La démarche pédagogique représentationnelle présentée par ces auteurs ne fait que mettre le focus sur la dimension sémiotique de l’enseignement et apprentissage des sciences. Les représentations et/ou modèles abordés ne sont pas (forcément) construits par les élèves, mais plutôt proposés par l’enseignant, expliqués, et surtout deviennent le centre de l’attention conjointe de l’enseignant et de ses élèves. Il s’agit donc d’une approche montrant le potentiel d’une attention accrue aux objets sémiotiques (graphe, croquis, image produite par des instruments, etc.) dans l’apprentissage des sciences.
Aborder les modèles comme des objets sémiotiques complexes pose la question de leur multimodalité : bien des modèles en physique requièrent de l’élève d’articuler des représentations graphiques ou visuelles, des écritures mathématiques, des explications verbales, etc. Ce défi a été relevé par Duval (1995), qui considère la tâche cognitive en jeu dans un cadre théorique piagétien : il s’agit pour l’apprenant de réussir à coordonner divers registres sémiotiques. Duval propose un “modèle opératoire de la représentation » (1995, p.65) basé sur les travaux de Bresson, permettant une description des systèmes complexes que sont les modèles. Cette approche permet de mettre en évidence qu’il est nécessaire, pour enseigner au sujet d’un référent non perceptible (comme c’est souvent le cas en physique), d’utiliser au moins deux registres sémiotiques différents et de les coordonner ensemble. C’est ce qu’une modélisation permet de faire. Dans cette analyse sémiotique, la coordination de divers registres sémiotiques apparaît comme un des rôles importants et spécifiques à la modélisation et aux modèles.
La modélisation en tant qu’opération cognitive
De nombreux travaux de psychologie cognitive se réfèrent aux modèles mentaux des élèves, notamment dans le courant de recherche s’intéressant au changement conceptuel (conceptual change). Les modèles désignent alors quelque chose de l’ordre de la représentation ou de l’image mentale (Piaget), et la modélisation fait référence à une opération cognitive des élèves. Si toute opération cognitive demeure par nature impossible à observer directement, il convient néanmoins de souligner ce sur quoi les chercheurs se basent pour inférer de telles opérations chez l’élève. Or, ces inférences se basent finalement sur la production des élèves, sans prendre en compte la médiation par le langage, et cette production, si elle est l’indice d’opérations cognitives, ne se réduit pas à de telles opérations et comprend d’autres dimensions constitutives (voir par exemple Tiberghien, 2003). En particulier, nous aimerions souligner l’importance de l’usage et des résistances exercées par le matériel, d’une part, et l’importance des usages et du développement d’outils sémiotiques permettant une médiation de la pensée, d’autre part. La question de la coordination des registres sémiotiques mise en évidence ci-dessus mériterait également une discussion plus approfondie.
Nous cherchons donc ici une démarche plus descriptive que celle qui consiste à catégoriser les élèves en fonction de leurs performances dans des modèles mentaux ou opérations définies a priori par les chercheurs. Une manière d’aborder la dimension cognitive de l’activité de modélisation dans une démarche descriptive consiste à analyser les étapes de la construction d’un modèle, telles qu’elles sont mises en œuvre par les élèves lorsque ce sont eux qui dirigent cette construction.
Le processus de modélisation : les étapes d’une construction
Illustrons une telle approche par un exemple. L’enseignant demande à ses élèves de trouver la forme idéale d’une tête de moine. Cette modélisation ne part pas d’un modèle physique ou mathématique, mais d’un modèle mental (voir plus loin) quotidien, celui d’une forme à peu près cylindrique, un peu arrondie, à la manière d’un petit tonneau. Elle aboutira à un modèle théorique et mathématique, en commençant par un premier modèle physique issu de la question posée : la tête de moine idéale propose un maximum de fromage pour un minimum de croûte.
À ce stade, le modèle quotidien suffit déjà pour convaincre l’élève qu’il y a au moins une solution, quelque part entre le spaghetti et la crêpe, le seul paramètre physico-mathématique à contrôler étant le volume, à maintenir constant pendant l’évocation de la déformation.
Puis vient le modèle physique, double :
1. la tête de moine “est” un cylindre ;
2. la quantité de croûte “est” la surface de ce cylindre, et la quantité de fromage en “est” le volume.
« Oui, mais la croûte a tout de même une épaisseur ! » objectera peut-être un élève. Il offre là à son enseignant une occasion à ne pas manquer de lui expliquer ce qu’est, justement, un modèle !
Dans un premier temps, montrer qu’on a une solution possible c’est aussi la construction d’une démarche, d’abord qualitative, qui permet de composer le modèle petit à petit. Ensuite seulement se pose la question d’une modélisation numérique qui permettrait de fournir une réponse quantitative à la question, pour laquelle d’autres “gestes de modélisation” doivent être posés ; c’est la construction du modèle mathématique, par étapes :
1. Écriture de la question en termes de rayon et de hauteur du cylindre ;
2. Écriture de la surface et du volume en fonction du rayon et de la hauteur ;
3. Écriture de la contrainte du volume fixe ;
4. Obtention d’une fonction rayon ⟼ surface ;
5. La surface doit être minimale (équation) ;
6. Solution et conclusion.
Dans notre document vidéo du site web du dispositif mi-fini sur la modélisation en physique (Chabloz & Kohler, 2016), nous proposons une synthèse de ces étapes de construction.
Références
Bécu-Robinault, K. (2015). Un cadre épistemo-sémiotique pour concevoir des séances et analyser des pratiques d’étude et d’enseignement de la physique. Habilitation à diriger des recherches de l’Université de Toulouse, Éducation, Université Toulouse Jean-Jaurès.
Duval, R., (1995). Sémiosis et pensée humaine. Bern : P. Lang.
Giglio, M. (2015). Creative collaboration in teaching. London and New York : Palgrave Macmillan.
Gilbert, J. K. (2013). Representations and Models. In: Tytler, R., Prain, V., Hubber, P., and Waldrip, B. (Ed.), Constructing Representations to Learn in Science. (pp.193-198). Rotterdam, Boston, Taipei: Sense Publishers.
Grize, J.-B., (1982). De la logique à l’argumentation. Genève : Librairie Droz S.A.
Martinand, J.-L. (1996). Introduction à la modélisation. Actes du séminaire de didactique des disciplines technologiques, Cachan, Paris, FR : Liaison interuniversitaire pour la recherche en éducation scientifique et technologique.
Luc, C., & Durey, A. (1997). Modèles et modélisation dans les séquences de Travaux Pratiques sur le haut-parleur en classe de seconde. Didaskalia, 11, 39-73.
Lund, K., and Bécu-Robinault, K. (2010) La reformulation multimodale et polysémiotique comme aide à la compréhension de la physique. In : Rabatel, A. (Ed.), Analyse sémiotique et didactique des reformulations, Besançon : Presses universitaires de Franche-Comté.
Huber, P. and Tytler, K. (2013). Models and Learning Science. In: Tytler, R., Prain, V., Hubber, P., and Waldrip, B. (Ed.), Constructing Representations to Learn in Science. (pp.109-133). Rotterdam, Boston, Taipei: Sense Publishers.
Roy, P., & Hasni, A. (2014). Les modèles et la modélisation vus par des enseignants de sciences et technologies du secondaire au Québec. Revue des sciences de l’éducation de McGill, 49(2), 1-25.
Tiberghien, A. (2003). Des connaissances naïves au savoir scientifique. In : Kail, M., and Fayol, M. (Ed.), Les sciences cognitives et l’école, (pp. 353-413) Paris : PUF.
Tytler, R., Prain, V., Hubber, P., and Waldrip, B. (Ed.), (2013). Constructing Representations to Learn in Science. Rotterdam, Boston, Taipei: Sense Publishers.
Winther, J., (2006). Modèles et modélisation dans l’enseignement des sciences physiques. Le BUP physique chimie 884, 05/2006, 617-646.
[1] En effet, le mât d’un modèle réduit du Queen Anne’s Revenge du fameux pirate Barbe-Noire n’est pas vraiment un mât, mais plutôt un signifiant (en bois) dont le signifié est le mât du bateau représenté.

