coordination des objets et des registres sémiotiques
Bernard Chabloz
&
Alaric Kohler
Haute École Pédagogique BEJUNE
Pour citer ce document
Introduction
Des conventions d’écriture aux usages sémiotiques courants, en passant par quelques bizarreries traditionnelles qui ne le sont plus quand on a l’habitude, les exemples ci-dessous permettent de montrer que non seulement un signe peut être difficile à interpréter, certains objets sémiotiques comme la flèche jouer des rôles différents sans toujours fournir d’indice pour les inférer, mais en plus il est parfois nécessaire de coordonner plusieurs objets éventuellement de plusieurs registres sémiotiques différents pour, finalement, accéder au sens…
Pour chacun des exemples ci-dessous, nous tenterons de porter un regard de novice sur des outils sémiotiques d’expert ou des habitudes de langages génératrices d’ambiguïtés, de manière à mettre en perspective des manières de faire souvent issues d’une longue tradition disciplinaire dont les tenants et aboutissants n’échappent pas seulement au profane …
Nous décrirons quelques risques de malentendus sous la forme d’histoires drôles, et proposerons au moins une piste pour éviter ces écueils: la coordination des registres sémiotiques (Duval, 1995).
Premier exemple
Une étudiante passant un oral de physique (E. Jeannet, 1983, communication personnelle) tente de retrouver pourquoi un caillou lâché du sommet de la tour Eiffel ne retombe théoriquement (le modèle est celui de la chute libre) pas à la verticale de son point de départ. Face à l’insistance de son enseignant, l’étudiant dessine un long trait vertical du haut au bas de la feuille (cf. figure 1) : le caillou tombe…
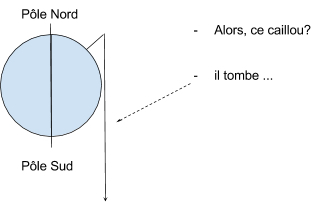
Figure 1. Question de l’enseignant et réponse de l’étudiante.
L’ambiguïté que génèrent les mots vertical, haut et bas est bien sûr le moteur de cette histoire drôle. On peut rappeler aux élèves qu’en général l’altitude du haut de leur feuille est la même que celle du bas. Et enchaîner avec cette question qui les surprend systématiquement:
● Pourquoi l’attraction terrestre est-elle verticale et pointe-t-elle vers le bas ?
La réponse est déroutante, précisément parce que le questionnement du statut d’un énoncé ne fait pas partie des habitudes scolaires: l’attraction terrestre est verticale et pointe vers le bas par définition des mots vertical et bas !
Cette ambiguïté n’est cependant pas seulement linguistique: le malentendu se situe dans la coordination entre des conventions de dessin lié à l’objet qu’est la feuille de papier, qui définit une certaine verticalité, et la verticalité en physique, qui est déterminée par le sens de la force de gravitation – en tout cas tant que l’on est à la surface d’une planète, le terme n’ayant plus tellement de sens dans l’espace où des gravités de sens et direction variées interagissent.
Deuxième exemple
Des élèves de première année de maturité académique au Lycée Jean-Piaget sont confrontés à une tâche “hameçon”, destinée à leur rendre nécessaire la pêche aux outils trigonométriques.
● Évaluez la pertinence de l’injonction neuchâteloise : « Rasez les Alpes, qu’on voie la mer ! ».
Les élèves constatent en quelques minutes qu’à cause de la courbure de la surface terrestre raser les Alpes ne suffira probablement pas à un Neuchâtelois pour voir la mer à Gênes, et qu’il lui faudra sans doute s’élever quelque peu pour que le bord de mer à Gênes soit dans sa ligne d’horizon. Ils schématisent alors la contrainte, et certains d’entre eux produisent un schéma, dont une version générique est présentée ci-dessous (figure 2).
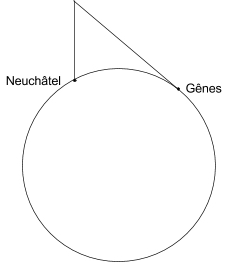
Figure 2. Schéma simplifié de quelques élèves
Il s’agit bien sûr d’une nouvelle version de l’histoire drôle de l’exemple 1. Cette fois, c’est une coordination des points de vue – tout à fait au sens des expériences piagétiennes – que l’élève doit réussir pour s’approprier l’une des conséquences de la rotondité de la Terre: le point de vue de l’observateur, coordonné à un point de vue très éloigné de la Terre, permet d’esquisser un schéma comme celui de la figure 2 et de remettre en cause l’injonction neuchâteloise.
Troisième exemple
La trajectoire d’un objet (lancé) en chute libre est une (partie de) parabole, c’est bien connu: voir la parabole de gauche sur la figure 3. Mais le graphe de l’horaire d’une chute libre verticale est également une parabole : voir la parabole de droite sur la figure 3.
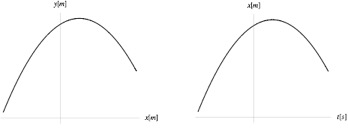
Figure 3. Dessins du graphe de la trajectoire d’un objet lancé en chute libre (abscisses et ordonnées en mètres) et du graphe de l’horaire d’une chute libre verticale (abscisses en secondes et ordonnées en mètres).
Le risque d’ambiguïté est patent: le dessin du graphe mobilisant immédiatement une représentation spatiale ou spatio-temporelle, le second graphe sera interprété comme le premier, soit comme une trajectoire. Deux remarques s’imposent.
1. La chute libre du physicien est le mouvement d’un point matériel en l’absence de toute autre force que la pesanteur, ou dans un cas de figure où les autres forces se compensent exactement (ce qu’une simulation vise); il ne s’agit donc pas d’un saut sans parachute…
2. Un graphe n’est pas un dessin (même si le choix du mot graphe n’est sans doute pas innocent…); dessin du graphe est donc écrit ici à dessein, comme une nouvelle provocation à visée didactique.
Ici aussi, la coordination est à l’oeuvre. D’abord celle du parcours de l’objet (lancé verticalement vers le haut) et de son horaire : une simulation graphique peut montrer la synchronisation de deux mouvements, celui du point (l’objet) sur sa trajectoire et celui du point (qui n’est plus l’objet, mais sa “position“ dans l’espace-temps) sur le graphe de son horaire. Ensuite, une coordination à un autre niveau permet aux élèves de s’approprier la parabole à la fois en tant qu’objet mathématique indépendant d’un référent (une parabole ne dénote ni une trajectoire, ni un horaire, etc. de manière générale et conventionnelle) et en tant qu’outil sémiotique jouant un rôle spécifique, et précisément distinct dans les deux exemples de paraboles ci-dessus (cf. figure 3).
Quatrième exemple
Voici un schéma électrique (figure 4) présentant le montage de résistances et d’une source d’électricité de 12 Volts.
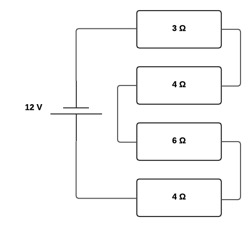
Figure 3. Schéma électrique.
Les résistances sont montées en série, même si le dessin les montre parallèles.
Remarque: le mot résistance est utilisé ici de façon métonymique puisqu’il désigne un objet qui a une résistance, c’est-à-dire une caractéristique physique traduite par un nombre, et dont le nom provient du processus homonyme. Que d’ambiguïtés en perspective !
Cinquième exemple
L’extrait de Formulaires et tables (CRM, 2015) présenté par la figure 5 montre quatre relations entre grandeurs physiques dans le domaine de l’électrocinétique.

Figure 3. Relations entre grandeurs physiques en électrocinétique, extrait de CRM, 2015, p.148.
Rien n’indique une différence de statut entre ces énoncés, et pourtant celui de l’un d’entre eux est essentiellement différent. En effet, par définition de ces grandeurs, la puissance électrique (PAB) consommée (ou fournie) par un élément est le produit de la tension électrique (UAB) à ses bornes par l’intensité du courant (I) qui le traverse. Cet énoncé est donc toujours vrai, au contraire des trois autres, qui relèvent de la loi d’Ohm, laquelle, comme toute loi physique, est une hypothèse !
Références
Commission Romande de Physique (2015/1985). Formulaires et tables. Genève: Éditions du Tricorne.
